Decision Tree algorithm belongs to the family of supervised learning algorithms. Unlike other supervised learning algorithms, decision tree algorithm can be used for solving regression and classification problems too.
The general motive of using Decision Tree is to create a training model which can use to predict class or value of target variables by learning decision rules inferred from prior data(training data).
The understanding level of Decision Trees algorithm is so easy compared with other classification algorithms. The decision tree algorithm tries to solve the problem, by using tree representation. Each internal node of the tree corresponds to an attribute, and each leaf node corresponds to a class label.
Decision Tree classifier, Image credit: www.packtpub.com
In decision trees, for predicting a class label for a record we start from the root of the tree. We compare the values of the root attribute with record’s attribute. On the basis of comparison, we follow the branch corresponding to that value and jump to the next node.
We continue comparing our record’s attribute values with other internal nodes of the tree until we reach a leaf node with predicted class value. As we know how the modeled decision tree can be used to predict the target class or the value. Now let’s understanding how we can create the decision tree model.
The below are the some of the assumptions we make while using Decision tree:
Decision tree model example Image Credit: http://zhanpengfang.github.io/
Decision Trees follow Sum of Product (SOP) representation. For the above images, you can see how we can predict can we accept the new job offer? and Use computer daily? from traversing for the root node to the leaf node.
It’s a sum of product representation. The Sum of product(SOP) is also known as Disjunctive Normal Form. For a class, every branch from the root of the tree to a leaf node having the same class is a conjunction(product) of values, different branches ending in that class form a disjunction(sum).
The primary challenge in the decision tree implementation is to identify which attributes do we need to consider as the root node and each level. Handling this is know the attributes selection. We have different attributes selection measure to identify the attribute which can be considered as the root note at each level.
The popular attribute selection measures:
If dataset consists of “n” attributes then deciding which attribute to place at the root or at different levels of the tree as internal nodes is a complicated step. By just randomly selecting any node to be the root can’t solve the issue. If we follow a random approach, it may give us bad results with low accuracy.
For solving this attribute selection problem, researchers worked and devised some solutions. They suggested using some criterion like information gain, gini index, etc. These criterions will calculate values for every attribute. The values are sorted, and attributes are placed in the tree by following the order i.e, the attribute with a high value(in case of information gain) is placed at the root.
While using information Gain as a criterion, we assume attributes to be categorical, and for gini index, attributes are assumed to be continuous.
By using information gain as a criterion, we try to estimate the information contained by each attribute. We are going to use some points deducted from information theory.
To measure the randomness or uncertainty of a random variable X is defined by Entropy.
For a binary classification problem with only two classes, positive and negative class.
By calculating entropy measure of each attribute we can calculate their information gain. Information Gain calculates the expected reduction in entropy due to sorting on the attribute. Information gain can be calculated.
To get a clear understanding of calculating information gain & entropy, we will try to implement it on a sample data.
We are going to use this data sample. Let’s try to use information gain as a criterion. Here, we have 5 columns out of which 4 columns have continuous data and 5th column consists of class labels.
A, B, C, D attributes can be considered as predictors and E column class labels can be considered as a target variable. For constructing a decision tree from this data, we have to convert continuous data into categorical data.
We have chosen some random values to categorize each attribute:
| A | B | C | D |
| >= 5 | >= 3.0 | >= 4.2 | >= 1.4 |
| < 5 | < 3.0 | < 4.2 | < 1.4 |
There are 2 steps for calculating information gain for each attribute:
The entropy of Target: We have 8 records with negative class and 8 records with positive class. So, we can directly estimate the entropy of target as 1.
| Variable E | |
| Positive | Negative |
| 8 | 8 |
Calculating entropy using formula:
E(8,8) = -1*( (p(+ve)*log( p(+ve)) + (p(-ve)*log( p(-ve)) )
= -1*( (8/16)*log2(8/16)) + (8/16) * log2(8/16) )
= 1
Var A has value >=5 for 12 records out of 16 and 4 records with value <5 value.
Entropy(Target, A) = P(>=5) * E(5,7) + P(<5) * E(3,1)
= (12/16) * 0.9799 + (4/16) * 0.81128 = 0.937745
Var B has value >=3 for 12 records out of 16 and 4 records with value <5 value.
Entropy(Target, B) = P(>=3) * E(8,4) + P(<3) * E(0,4)
= (12/16) * 0.39054 + (4/16) * 0 = 0.292905
Var C has value >=4.2 for 6 records out of 16 and 10 records with value <4.2 value.
Entropy(Target, C) = P(>=4.2) * E(0,6) + P(< 4.2) * E(8,2)
= (6/16) * 0 + (10/16) * 0.72193 = 0.4512
Var D has value >=1.4 for 5 records out of 16 and 11 records with value <5 value.
Entropy(Target, D) = P(>=1.4) * E(0,5) + P(< 1.4) * E(8,3)
= 5/16 * 0 + (11/16) * 0.84532 = 0.5811575
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
From the above Information Gain calculations, we can build a decision tree. We should place the attributes on the tree according to their values.
An Attribute with better value than other should position as root and A branch with entropy 0 should be converted to a leaf node. A branch with entropy more than 0 needs further splitting.
Gini Index is a metric to measure how often a randomly chosen element would be incorrectly identified. It means an attribute with lower gini index should be preferred.
Example: Construct a Decision Tree by using “gini index” as a criterion
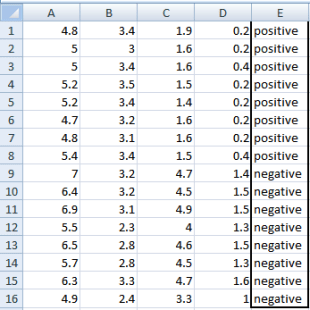We are going to use same data sample that we used for information gain example. Let’s try to use gini index as a criterion. Here, we have 5 columns out of which 4 columns have continuous data and 5th column consists of class labels.
A, B, C, D attributes can be considered as predictors and E column class labels can be considered as a target variable. For constructing a decision tree from this data, we have to convert continuous data into categorical data.
We have chosen some random values to categorize each attribute:
| A | B | C | D |
| >= 5 | >= 3.0 | >=4.2 | >= 1.4 |
| < 5 | < 3.0 | < 4.2 | < 1.4 |
Var A has value >=5 for 12 records out of 16 and 4 records with value <5 value.
By adding weight and sum each of the gini indices:
Var B has value >=3 for 12 records out of 16 and 4 records with value <5 value.
Var C has value >=4.2 for 6 records out of 16 and 10 records with value <4.2 value.
Var D has value >=1.4 for 5 records out of 16 and 11 records with value <1.4 value.
|
|
||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
Overfitting is a practical problem while building a decision tree model. The model is having an issue of overfitting is considered when the algorithm continues to go deeper and deeper in the to reduce the training set error but results with an increased test set error i.e, Accuracy of prediction for our model goes down. It generally happens when it builds many branches due to outliers and irregularities in data.
Two approaches which we can use to avoid overfitting are:
In pre-pruning, it stops the tree construction bit early. It is preferred not to split a node if its goodness measure is below a threshold value. But it’s difficult to choose an appropriate stopping point.
In post-pruning first, it goes deeper and deeper in the tree to build a complete tree. If the tree shows the overfitting problem then pruning is done as a post-pruning step. We use a cross-validation data to check the effect of our pruning. Using cross-validation data, it tests whether expanding a node will make an improvement or not.
If it shows an improvement, then we can continue by expanding that node. But if it shows a reduction in accuracy then it should not be expanded i.e, the node should be converted to a leaf node.
![H(X)=\mathbb {E} _{X}[I(x)]=-\sum _{x\in \mathbb {X} }p(x)\log p(x).](https://wikimedia.org/api/rest_v1/media/math/render/svg/971ffd75b32f284123036d4ae8fc3dd6e377e030)
